1618. Наибольшая общая подпоследовательность
Даны две
последовательности. Найдите длину их наибольшей общей подпоследовательности.
Подпоследовательность
– это
последовательность, которая может быть получена из исходной последовательности
удалением некоторых элементов без изменения порядка оставшихся.
Вход. В первой строке задано целое число n (1 ≤ n
≤ 1000) – длина первой последовательности.
Во второй строке записаны n целых чисел – элементы первой
последовательности, каждое из которых по модулю не превышает 104.
В третьей
строке задано целое число m (1 ≤ m ≤ 1000) – длина второй последовательности.
В четвертой строке записаны m целых чисел – элементы второй последовательности, каждое
из которых по модулю не превышает 104.
Выход. Выведите одно целое число –
длину наибольшей общей подпоследовательности двух заданных последовательностей.
|
Пример
входа |
Пример
выхода |
|
3 1 2 3 4 2 1 3 5 |
2 |
РЕШЕНИЕ
динамическое
программирование
Наибольшая
Общая Подпоследовательность
Анализ алгоритма
Подпоследовательность
заданной последовательности – это набор элементов, расположены в том же
порядке, что и в исходной последовательности, но не обязательно подряд. Подпоследовательность
может быть получена из исходной последовательности путем удаления некоторых её
элементов.
Например, рассмотрим последовательность {2, 1, 3, 5}. Тогда
·
{1, 5}, {2}, {2, 3, 5} являются подпоследовательностями;
·
{5, 1}, {2, 3, 1} не являются подпоследовательностями;
Общая подпоследовательность двух
последовательностей – это подпоследовательность, которая встречается в обеих последовательностях.
Наибольшая
общая подпоследовательность (НОП) – это общая подпоследовательность максимальной
длины.
Например, наибольшей
общей подпоследовательностью последовательностей {1, 2, 3} и {2, 1, 3, 5} могут
быть {1, 3} или {2, 3}. Длина НОП в этом случае равна
2.
Пусть f(i,
j) – длина наибольшей общей подпоследовательности (НОП) для префиксов
последовательностей x1x2…xi и y1y2…yj.
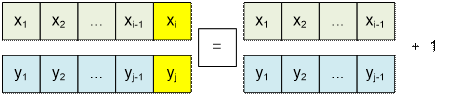
Если xi ¹ yj, то НОП следует искать среди двух
вариантов:
·
префиксов x1x2…xi
и y1y2…yj-1 (их НОП равен f(i, j
– 1)),
·
префиксов x1x2…xi-1 и y1y2…yj
(их НОП равен f(i – 1, j)).
Возвращаем максимальное из значений:
f(i, j) = max( f(i,
j – 1), f(i – 1, j) )

Если xi = yj, то добавляем текущий
элемент xi в НОП и рассматриваем более короткие
префиксы x1x2…xi-1 и y1y2…yj-1:
f(i, j) = 1 + f(i –
1, j – 1)
Если одна из
последовательностей пустая, то их НОП тоже пустая:
f(0, j) = f(i, 0) = 0
Рекуррентное
соотношение для вычисления длины НОП выглядит следующим образом:
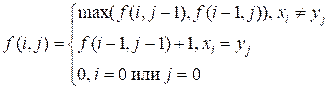
Значения f(i,
j) будем хранить в массиве m[0..1000, 0..1000], где m[0][i] = m[i][0]
= 0. Каждая следующая
строка массива m[i][j] вычисляется через предыдущую. Таким образом, для
нахождения ответа достаточно сохранять в памяти только две строки длины 1000.
Пример
Пусть X = abcdgh,
Y = aedfhr. Наибольшей общей подпоследовательностью будет adh, ее
длина равна f(6, 6) = 3.
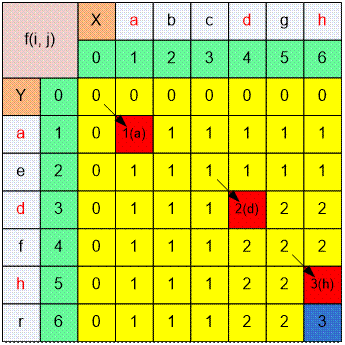
f(6, 6) = max(f(6, 5),
f(5, 6)) = max(2, 3) = 3, так как Y[6] = r ≠ h = X[6].
f(5, 6) = 1 + f(4, 5) = 1
+ 2 = 3, так как Y[5] = h = X[6].
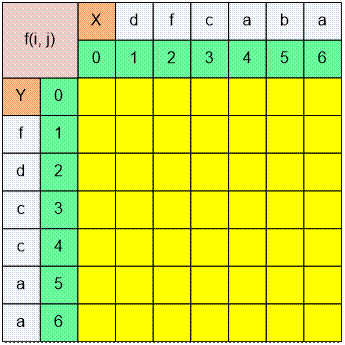
Заполните следующую таблицу:
Реализация алгоритма
Массивы x
и y содержат входные последовательности, а n и m – их длины. Массив mas содержит две
последние строки динамического преобразования.
#define SIZE 1010
int x[SIZE], y[SIZE], mas[2][SIZE];
Читаем входные
последовательности в массивы, начиная с первого индекса, то есть в ячейки x[1..n] и y[1..m].
scanf("%d",&n);
for (i = 1; i <=
n; i++) scanf("%d",&x[i]);
scanf("%d",&m);
for (i = 1; i <=
m; i++) scanf("%d",&y[i]);
Обнуляем массив mas.
memset(mas,0,sizeof(mas));
Вычисляем значения функции f(i, j).
Изначально mas[0][j] содержит
значения f(0, j) = 0. Далее в mas[1][j] заносим значения f(1, j).
Поскольку для вычисления f(2, j) достаточно иметь значения предыдущей
строки массива mas, то значения f(2, j)
можно сохранить в ячейках mas[0][j],
значения f(3, j) – в ячейках mas[1][j] и так далее.
for (i = 1; i <=
n; i++)
for (j = 1; j <=
m; j++)
if (x[i] ==
y[j])
mas[i%2][j] = 1 +
mas[(i+1)%2][j-1];
else
mas[i%2][j] =
max(mas[(i+1)%2][j],mas[i%2][j-1]);
Выводим ответ, который находится в
ячейке mas[n][m]. Первый аргумент вычисляем по модулю 2.
printf("%d\n",mas[n%2][m]);
Реализация алгоритма – рекурсия
#include <stdio.h>
#include <string.h>
#define SIZE 1002
int x[SIZE], y[SIZE],
dp[SIZE][SIZE];
int n, m, i, j, res;
int max(int i, int j)
{
return (i >
j) ? i : j;
}
int lcs(int *x, int *y, int m, int n)
{
if (m == 0
|| n == 0)
return 0;
if (dp[m][n] !=
-1) return dp[m][n];
if (x[m] == y[n])
return dp[m][n] = 1
+ lcs(x, y, m - 1,
n - 1);
else
return dp[m][n] =
max(lcs(x, y, m, n -
1), lcs(x, y, m - 1,
n));
}
int main(void)
{
scanf("%d",
&n);
for (i =
1; i <= n; i++) scanf("%d", &x[i]);
scanf("%d",
&m);
for (i =
1; i <= m; i++) scanf("%d", &y[i]);
memset(dp,
-1, sizeof(dp));
res =
lcs(x, y, n, m);
printf("%d\n",
res);
return 0;
}
Java реализация
import java.util.*;
public class Main
{
static int x[], y[], dp[][];
static int n, m;
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
n = con.nextInt();
x = new int[n+1];
for
(int i = 1;
i <= n; i++)
x[i] = con.nextInt();
m = con.nextInt();
y = new int[m+1];
for
(int i = 1;
i <= m; i++)
y[i] = con.nextInt();
dp = new int[2][m+1];
for
(int i = 1;
i <= n; i++)
for
(int j = 1;
j <= m; j++)
if (x[i] == y[j])
dp[i%2][j] = 1
+ dp[(i-1)%2][j-1];
else
dp[i%2][j] =
Math.max(dp[(i-1)%2][j],dp[i%2][j-1]);
System.out.println(dp[n%2][m]);
con.close();
}
}
Java реализация – рекурсия
import java.util.*;
public class Main
{
static int x[], y[], dp[][];
static int n, m;
public static int lcs(int m, int n)
{
if (m == 0
|| n == 0)
return 0;
if (dp[m][n] !=
-1) return dp[m][n];
if (x[m] == y[n])
return dp[m][n] = 1
+ lcs(m - 1, n - 1);
else
return dp[m][n] =
Math.max(lcs(m, n -
1), lcs(m - 1, n));
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
n = con.nextInt();
x = new int[n+1];
for
(int i = 1;
i <= n; i++)
x[i] = con.nextInt();
m = con.nextInt();
y = new int[m+1];
for
(int i = 1;
i <= m; i++)
y[i] = con.nextInt();
dp = new int[n+1][m+1];
for
(int i = 0;
i <= n; i++)
Arrays.fill(dp[i],
-1);
int res = lcs(n,m);
System.out.println(res);
con.close();
}
}
Python реализация
Читаем входные последовательности в списки x и y.
n = int(input())
x = [0] + list(map(int, input().split()))
m = int(input())
y = [0] + list(map(int, input().split()))
Инициализируем список dp, который содержит
две последние строки динамического преобразования.
dp = [[0] * (m + 1) for _ in range(2)]
Вычисляем значения f(i, j) (1 ≤ i ≤ n,
1 ≤ j ≤ m). Результаты f(i,
j) сохраняем в ячейках dp[i % 2][j].
for i in range(1, n + 1):
for j in range(1, m + 1):
if x[i] == y[j]:
dp [i % 2][j] = dp[(i - 1) % 2][j - 1] + 1
else:
dp[i % 2][j] = max(dp[(i - 1) % 2][j], dp[i % 2][j - 1])
Выводим ответ, который находится в ячейке dp[n][m]. Первый аргумент вычисляем
по модулю 2.
print(dp[n % 2][m])

